LISN: Interdisciplinary Numerical Sciences Laboratory
Paris-Saclay research lab primarily active in Data and Engineering Sciences with interdisciplinary themes: AI, fluid mechanics, human-computer interaction, language processing, and bioinformatics
NEW POSTDOC position: First semester 2024 ANR THERMAL postdoc position opening! Physics-informed machine learning super-resolution in highly turbulent natural convection
CALL: SPECIAL ISSUE of COMPUTER PHYSICS COMMUNICATIONS about "Advances in physics aware machine learning", DEADLINE OCTOBER 1st 2024
The scope covers research papers in: • Machine learning-based reduced order modelling techniques for high-dimensional systems • Methodology development for Physics-informed neural networks (PINNs) • Theory or novel applications of machine learning algorithms with data assimilation for high-dimensional physics systems • Physics aware uncertainty quantification and sensitivity analysis for data-driven models • Machine learning in the spectral domain for complex physics problems
Bienvenu(e)!
I am a CNRS research director and deputy director of the LISN lab on Paris-Saclay campus in Orsay. I'm a member of the DATAFLOT (DAta science, TrAnsition, FLuid instabiLity, contrOl & Turbulence) research group of the Mechanical Engineering department.
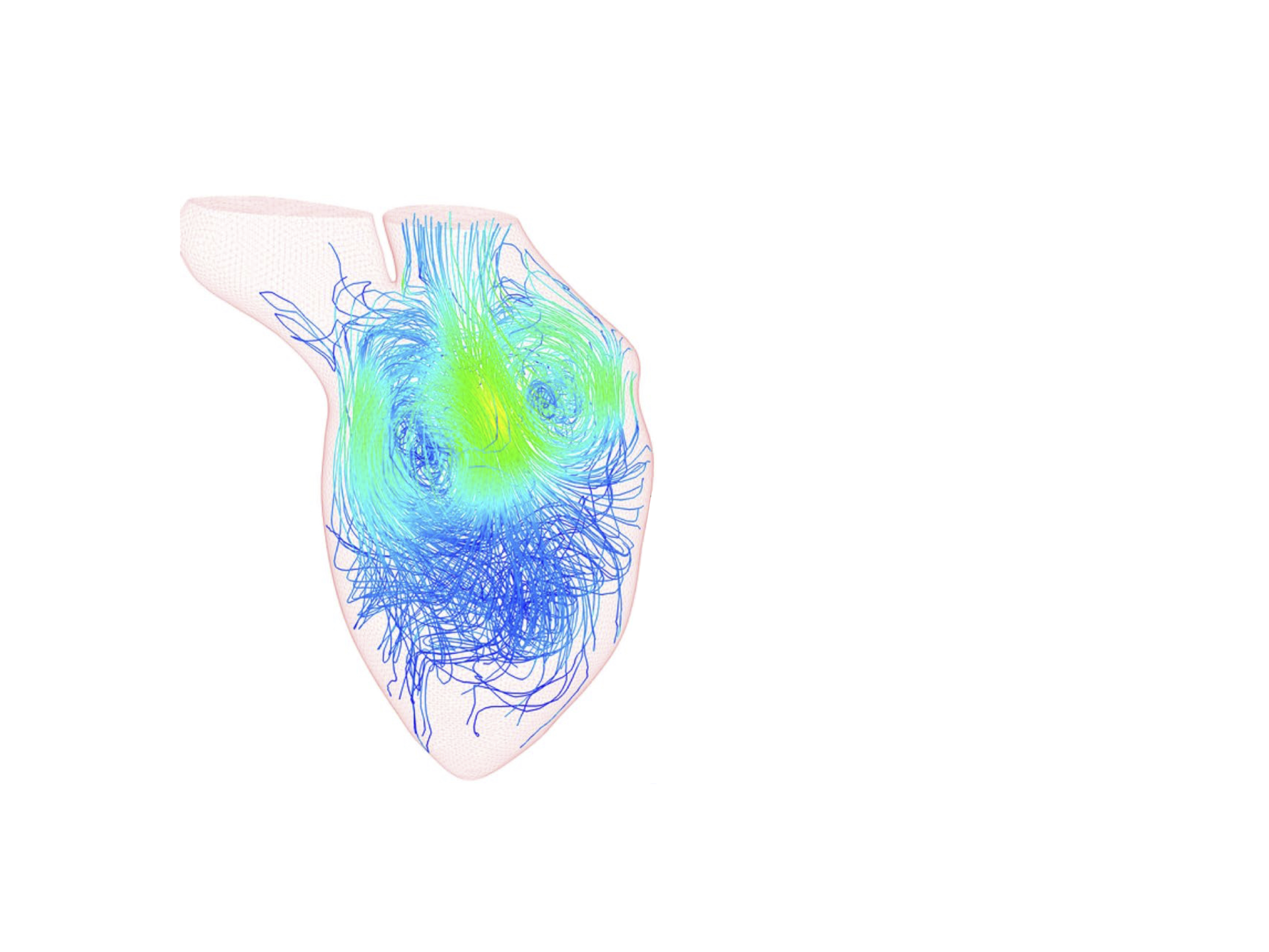
My research interests relate to stochastic modeling and computational mechanics, with emphasis on: physics-informed statistical learning, reduced-order modeling, uncertainty quantification, data assimilation, sensitivity analysis and robust optimization.Applications in computational mechanics range from turbulence modeling, heat transfer, flow-structure interaction problems to biomechanics, environmental flows and fluid mechanics related to the energy sector.

Physics-Informed Machine Learning:
CHECK-OUT this new Stochastic Environmental Research and Risk Assessment paper ! [Nony et al, SERRA 2023]
The big data and machine learning revolution is gaining traction in the fluid mechanic community as it has changed the way turbulent data can be analyzed to more effectively extract knowledge from it. It becomes now possible to use deep learning to speedup or to (partly) substitute traditional fluid flow PDEs, which were expensive to solve. Nevertheless, generalization errors of those models are considerably improved if some "physics information" (in the form of invariant, first principles, symmetries, etc...) is included/enforced in order to regularize the training. Some effort is put to develop new ML methods along those lines, towards advanced methods for model-order reduction, system identification, PDE solver substitutes and turbulence closures.
Uncertainty quantification (UQ) for Computational Fluid Dynamics (CFD)
Thanks to the rapidly growing computational resources and improvements in numerical/experimental techniques, increasingly complex CFD problems are nowadays investigated. Assessing and optimizing the accuracy and reliability of numerical predictions has become a challenge of utmost importance. Due to the interdisciplinarity nature of UQ, this topic is also connected to the adjacent areas of statistics, high-performance computing, and the analysis of partial differential equations with random input data.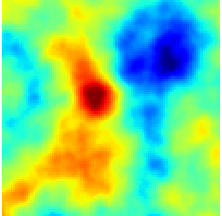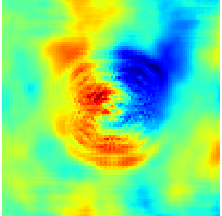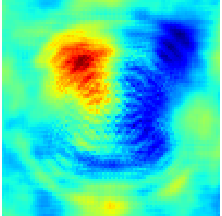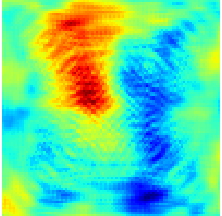 Data assimilation of a noisy shallow water system, [Cheng et al, SERRA 2019].
Data assimilation of a noisy shallow water system, [Cheng et al, SERRA 2019].
Data assimilation and inverse problems
The idea is to leverage the information contained in various data sources in order to improve our numerical models. The model is for instance complemented with data coming from additional physical/numerical experiments. The "data-enhanced" updated model can be made “data-frugal” thanks to specifics of the physical systems. Efficient data-driven methods scale with the effective dimension of the problem, as opposed to the ambient dimension, while naturally enjoying some robustness, a crucial aspect in practical applications.